Volume of Hollow Cylinder: its Formula, Surface Area & 2 Examples

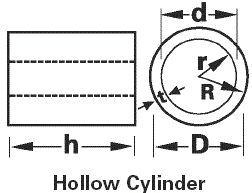
In the case of the volume of a hollow cylinder, we measure two radii one for the inner circle and other for the outer circle formed by the base of the hollow cylinder.

The cylinder is one of the most basic curvilinear geometric shapes and the surface is established by the point at a fixed distance from a given line segment and the hollow cylinder is a type of cylinder that is hollow and it has two radii such as R is external or outer radius and r is the inside or internal radius.

The Formula for Volume of Hollow Cylinder:

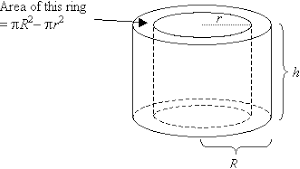
Let suppose that R and r are the two radii of the given hollow cylinder with the height ‘h’, then the volume of this cylinder can be written as:

V = πh (R² – r²)

Where,

1. V is the volume of the outer surface
2. h is the height
3. R is the radius of the outer surface and
4. r is the radius of the inner surface.

Surface Area of Hollow Cylinder:

The surface area of the cylinder is the amount of square units required to cover the surface of the cylinder and formula for the surface area of the cylinder is equal to the total surface area of the bases of the cylinder and surface area of its sides and given as;

Surface Area = 2πrh + 2πRh + 2(πR² – πr²)

Where R is the radius of the outer surface while r is the radius of the inner surface.

Examples of Volume of Hollow Cylinder:

• A hollow cylinder having 21m height, 4m outer radius of the surface of hollow cylinder & 3m inner radius of the surface. Find the volume of the hollow cylinder.

Given Data;

As we know π = 22/7

The radius of outer surface R = 4m

The radius of the inner surface, r = 3m

Height h = 21m

The volume of hollow cylinder =?

Solution:

The Volume of hollow cylinder = πh (R2 – r2)

= 22/7 × 21 (4² – 3²)

= 462 m³

Let suppose, the cost of material per m³ is 100 rupees

Then,

Cost of material for 462 m³ = volume of pipe × cost of material per m³

= 462 × 100 = 46200 rupees

• There is a 210cm hollow cylinder copper pipe and its outer and inner diameters are 10cm and 6cm. Find the volume of copper used in making the pipe?

Given data:

h is the height of the cylindrical pipe = 210 cm

As,

The external radius R = 10/2 = 5 cm

Internal radius r = 6/2 = 3 cm

Solution:

Then,

Volume of the copper used in manufacturing the pipe = Volume of outer cylinder – volume of inner cylinder.

= πR²h – πr²h = π (R² – r²) h

= 22/7 [5² – 3²] × 210

= 22/7 × 16 × 210

= 22 × 16 × 30 = 10560 cu.cm